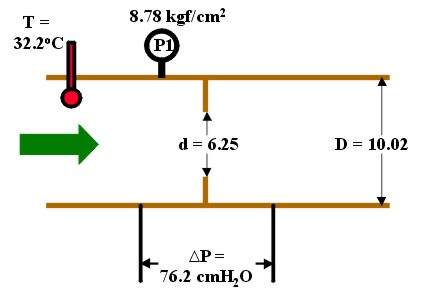
Exemplo 1 - Borda QuadradaAr comprimido saturado escoa numa tubulação de 10.02 pol diâ.
interno a uma pressão barométrica de 8.78 kgf/cm2 e a 32.2oC.
O diferencial de pressão é causado por um orifício (INOX 316) concênctrico de
bordas quadradas com tomadas de pressão na flange segundo normas ASME.
Considerando que o orifício com 6.250 pol de diâ. causa um diferencial de pressão é
de 76.2 cmH2O e a pressão barométrica é de 1.03 kgf/cm2; calcule
a vazão mássica do medidor.
Conversões:
D = 25.450 cm (10.02")
d = 15.875 cm (6.25")
mar = 8.15.10-5 (g/cm/s)
Variáveis que não variam durante cálculo
Razão Diâmetros:
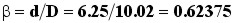
Const. E:
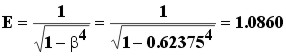
Pressão Abs. Montante:
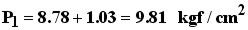
Razão Pressões:
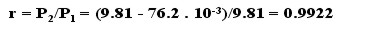
Razão Cal. Específicos:
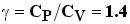
Coef. Expansão:
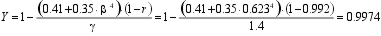
Densidade Mistura ar+vapor
Coef. Compressibilidade (9.81 kg/cm2
& 32.2oC) ® Z=0.998
Pressão sat. vapor a 32.2oC ® Pv = 0.045 kg/cm2;
Pressão parcial do ar na mistura ® Pa = 9.77 kg/cm2;
Umidade Relativa w = 0.622 Pv/Pa ® w = 0.0029 g[vap]/g[ar]
Const. Ar & vapor: Rar = 287 m2/s2/oK
e Rvap = 462 m2/s2/oK
Const. Mistura R = Rar + w.Rvap = 288.34
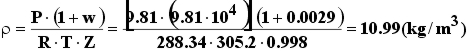
ou r1 =10.99.10-3
(g/cm3)
Variáveis determinadas
iterativamente
Vazão mássica:
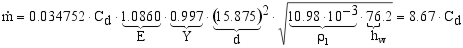
Reynolds Orifício:
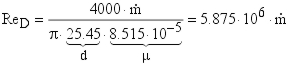
Coef. de Descarga

constantes geométricas:

Após substituições das variáveis chega-se a uma expressão
para a vazão mássica em função de Cd e do Cd em função da vazão mássica :
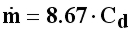
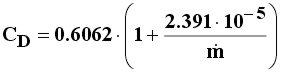
As duas equações podem ser resolvidas por substituição (as
vezes trabalhoso) ou iterativamente chutando-se um valor incial para Cd (0.65).
O processo iterativo é mostrado na tabela; uma iteração foi suficiente para chegar
ao valor correto!
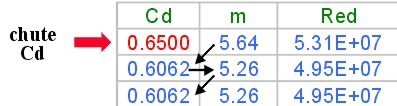
Resposta: a vazão mássica é 5.26 kg/seg de ar úmido.
A vazão volumétrica, Q*, na condição padrão 1atm & 21oC é:

|

