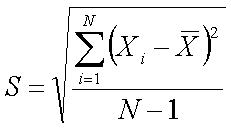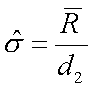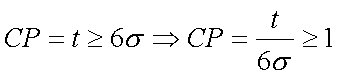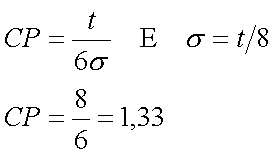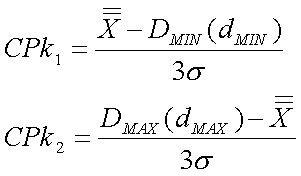CONTROLE ESTATÍSTICO DE PROCESSO

· HISTORICAMENTE, AS ORIGENS DO CEP ESTÃO EM 1924 COM AS PRIMEIRAS CARTAS DE CONTROLE DE SHEWART

· O USO INDUSTRIAL DO CEP TEM INÍCIO NA DÉCADA DE 50 APÓS A SEGUNDA GRANDE GUERRA MUNDIAL

· A PARTIR DA DÉCADA DE 70 O CEP DIFUNDIU-SE NA EUROPA, NOS EUA E PRINCIPALMENTE NO JAPÃO

· DOIS MÉTODOS DE CEP: MEDIDAS POR ATRIBUTOS (COR, AROMA, ASPECTO) E MEDIDAS POR VARIÁVEIS (DIMENSÕES, PESO)

· NO MÉTODO POR VARIÁVEIS AS MEDIDAS SÃO FEITAS COM INSTRUMENTOS PARA VERIFICAR SE O PRODUTO ENCONTRA-SE OU NÃO DENTRO DAS ESPECIFICAÇÕES DE FABRICAÇÃO

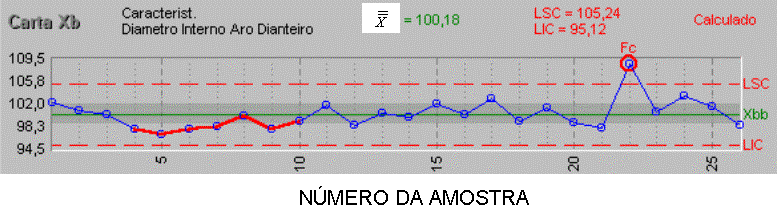
· PARA SE AVALIAR UM PROCESSO DE FABRICAÇÃO PELO CEP, É NECESSÁRIO QUE SEJAM CONHECIDAS E CONTROLADAS TODAS AS VARIÁVEIS QUE O INFLUENCIAM

· CONCEITOS BÁSICOS:

CARTA DE CONTROLE – PLOTAM-SE OS VALORES MÉDIOS DAS DIMENSÕES DAS AMOSTRAS (CADA AMOSTRA COM 5 RÉPLICAS) NA ORDENADA E O NÚMERO DA AMOSTRA NA ABSCISSA.

NA CARTA MOSTRADA:

É A MÉDIA ARITMÉTICA DAS MÉDIAS ARITMÉTICAS () DAS AMOSTRAS

LIC – LIMITE INFERIOR E CONTROLE

LSC – LIMITE SUPERIOR DE CONTROLE

ONDE A2 É TABELADO E IGUAL A 0,58 PARA UMA AMOSTRA COM

N = 5 RÉPLICAS (TAB. 8.1 PÁG. 71 – LIVRO DO PROF. OLÍVIO)

É O VALOR MÉDIO DA AMPLITUDE QUE É A MEDIDA MAIS SIMPLES DA DISPERSÃO DOS VALORES R CALCULADOS

R É CALCULADO PELA DIFERENÇA ENTRE O MAIOR VALOR E O MENOR VALOR ENCONTRADO PARA CADA AMOSTRA

OS LIMITES DE CONTROLE NÃO SÃO OS LIMITES ESPECIFICADOS PELOS AFASTAMENTOS SUPERIOR E INFERIOR DEFINIDOS NO PROJETO DO COMPONENTE.

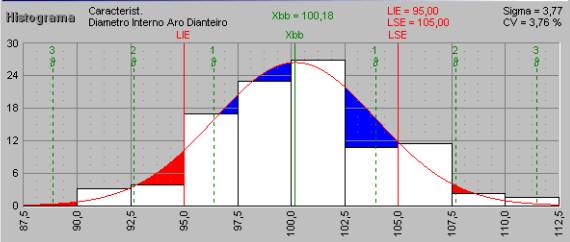
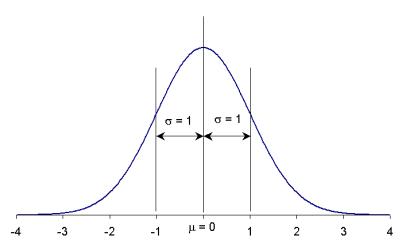
OS LIMITES DE CONTROLE REPRESENTAM A VARIABILIDADE DO PROCESSO DE FABRICAÇÃO E INDICAM QUAL A CAPACIDADE DE QUALIDADE DE TRABALHO QUE ESSE PROCESSO OFERECE.

· DISTRIBUIÇÃO NORMAL

UM PROCESSO DE FABRICAÇÃO PODE SER AVALIADO PELO CEP SE APRESENTAR OS RESULTADOS DISTRIBUÍDOS DE FORMA NORMAL.

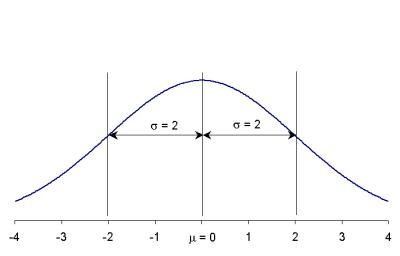
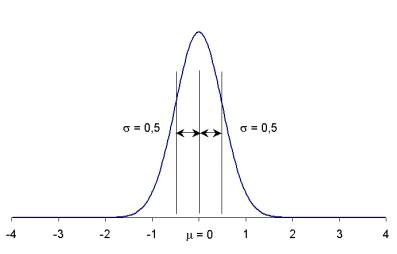
A DISTRIBUIÇÃO NORMAL EQUACIONADA POR GAUSS APRESENTA UM VALOR MÉDIO (m) E UM DESVIO-PADRÃO (s) QUE REPRESENTAM A POPULAÇÃO

QUANTO MAIOR O VALOR DE s MAIOR É A DISPERSÃO DOS RESULTADOS, OU SEJA, MAIOR É A VARIABILIDADE DO PROCESSO

NA FIGURA A SEGUIR, REPRESENTA-SE A CURVA NORMAL E O HISTOGRAMA CORRESPONDENTE AOS VALORES MEDIDOS

O DESVIO PADRÃO DA AMOSTRA (S) É CALCULADO PELA EXPRESSÃO:

JÁ O DESVIO PADRÃO DA POPULAÇÃO ANALISADA PODE SER ESTIMADO POR:

ONDE d₂ TAMBÉM É TABELADO EM FUNÇÃO DE N.

PARA N =5 TEM-SE d₂ = 2,33

NA CURVA NORMAL, O VALOR DE s É DADO PELO PONTO DE INFLEXÃO DA CURVA.

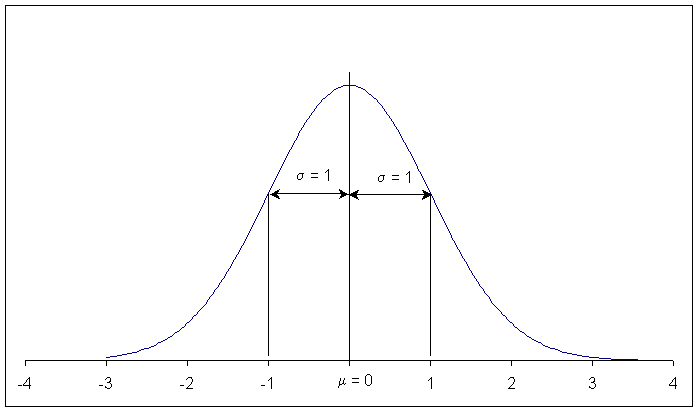
CURVA NORMAL PADRONIZADA: m = 0 E s = 1

A ÁREA SOB A CURVA NORMAL PADRÃO INDICA A PROBABILIDADE DE ENCONTRAR-SE VALORES ENTRE OS LIMITES ESPECIFICADOS.

ASSIM:

INTERVALO	PORCENTAGEM DE PEÇAS
	50%
	68,26%
	95,46%
	99,73%
	99,99%

· PARÂMETROS ESTATÍSTICOS DE UM PROCESSO

CAPACIDADE DO PROCESSO (CP)

É A CAPACIDADE QUE O PROCESSO TEM DE PRODUZIR PEÇAS EM QUE APENAS 0,27% DELAS ESTARÃO FORA DA TOLERÂNCIA (t) ESPECIFICADA. OU SEJA, O PROCESSO APRESENTA-SE DENTRO DE UM INTERVALO IGUAL A 6s:

A CAPACIDADE DO PROCESSO É DADA POR:

POR CONVENÇÃO, UM PROCESSO É CAPAZ QUANDO O DESVIO PADRÃO FOR MENOR QUE UM OITAVO DA TOLERÂNCIA ESPECIFICADA, DE MODO QUE A TOLERÂNCIA ABRANJA OITO OU MAIS DESVIOS PADRÕES, O QUE REPRESENTA UMA PROBABILIDADE DE 99,99% DE PRODUZIR-SE PEÇAS BOAS.

DESTE MODO, A CAPACIDADE DO PROCESSO PODE SER REDEFINIDA COMO:

ASSIM, UM PROCESSO SERÁ CAPAZ SE APRESENTAR UM VALOR DE CP MAIOR QUE 1,33

CAPACIDADE REAL DO PROCESSO (CPk)

SOMENTE A CAPACIDADE DO PROCESSO NÃO É SUFICIENTE PARA DETERMINAR SE O PROCESSO TEM SUA MÉDIA AJUSTADA CONFORME PROJETADA, OU SEJA, O PROCESSO PODE SER CAPAZ MAS APRESENTAR UMA MÉDIA INCORRETA (OU “FORA DE CENTRO”)

DOIS ÍNDICES SÃO DEFINIDOS:

ONDE DMIN (dMIN) E DMAX (dMAX) SÃO AS DIMENSÕES LIMITES ESPECIFICADAS NO PROJETO DO COMPONENTE AVALIADO

A CAPACIDADE REAL DO PROCESSO É O MENOR VALOR ENCONTRADO ENTRE CPk1 E CPk2.

O PROCESSO APRESENTARÁ BOA CAPACIDADE REAL QUANDO CPk FOR MAIOR QUE 1,33.

O PROCESSO ESTARÁ CENTRADO QUANDO CPk1 FOR IGUAL A CPk2.

EXEMPLO: PROCESSOS CENTRADOS MAS COM DESVIOS PADRÕES DIFERENTES