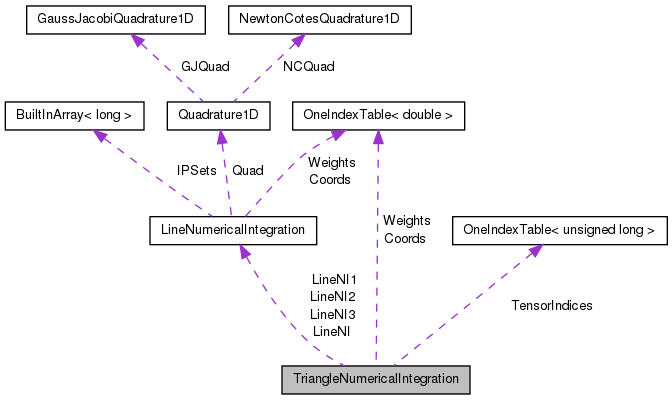
Calculates the coordinates and weights for numerical integration of the triangle element. The coordinates are those ones mapped from the square element to the baricentric coordinates of the triangle. More...

#include <TriangleNumericalIntegration.h>

Collaboration diagram for TriangleNumericalIntegration:

[legend]

List of all members.

Public Member Functions
	TriangleNumericalIntegration ()
	Default constructor.
	TriangleNumericalIntegration (TriangleNumericalIntegration &Instance)
	Copy-initializer constructor.
	~TriangleNumericalIntegration ()
	Class destructor.
TriangleNumericalIntegration &	operator= (TriangleNumericalIntegration &Instance)
	Copies the contents of instance to the object.
	operator LineNumericalIntegration & ()
	Cast operator for the reference of the class attribute "LineNI".
void	SetMaxPolyOrder (unsigned long MaxPolyOrder)
	Sets the maximum polynomial order.
void	SetNumberCoordsWeights (unsigned long NumberRow, unsigned long NumberData)
	Sets the coordinates and weights table for the specific TriangleNumericalIntegration allocated.
unsigned long	GetMaxPolyOrder ()
	Returns the maximum polynomial order.
LineNumericalIntegration &	GetLineNumericalIntegration (unsigned long LiDirection=1)
	Returns the reference to LineNumericalIntegration. According to LiDirection parameter returns one of the Line attributes of the class TriangleNumericalIntegration. If the direction is 0, it returns the numerical integration on the isoparametric coordinates.
unsigned long	GetNumberIntegrationPointsSets ()
	Returns the number of sets of integration points calculated using the polynomial and integration orders.
unsigned long	GetMaxNumberIntegrationPointsSets (unsigned long LiDirection=1)
	Returns the maximum number of sets of integration points according to LineNI[1-3] class attributes.
long	GetIntegrationPointsSetNumber (NumericalIntegrationAttributes_S &NIAttributes, unsigned long IntegrandOrder)
	Returns the set number of the integration points for the given polynomial order.
unsigned long	GetNumberIntegrationPoints (NumericalIntegrationAttributes_S &NIAttributes, ElementShape_E EntityShape, unsigned long IntegrandOrder, long &IntegPointsSetNumber)
	Returns the number of integration points given by integrand order for the quadrature rule stored in the class. Returns also the number of the set which stores the points.
unsigned long	GetNumberIntegrationPoints (ElementShape_E EntityShape, long IntegrationPointsSetNumber, unsigned long LiDirection=1)
	Returns the number of integration points for a given set number to a specific baricentric direction number.
unsigned long	GetTotalNumberIntegrationPoints ()
	Returns the total number of integration points.
double *const	GetIntegrationPointsCoords (NumericalIntegrationAttributes_S &NIAttributes, unsigned long EntityShape, unsigned long IntegrandOrder, unsigned long &NumberIntegPoints, unsigned long LiDirection=1)
	Returns the coordinates of the integration points. In the case of Shape=TRIANGLE, this method collects the coordinates for the triangle element from the coordinates of the line everytime the method is executed.
double *const	GetIntegrationPointsWeights (NumericalIntegrationAttributes_S &NIAttributes, ElementShape_E EntityShape, unsigned long IntegrandOrder, unsigned long &NumberIntegPoints, unsigned long LiDirection=1)
	Returns the weights of the integration points. This method assumes that the weights have been already calculated by the procedure RunNumericalIntegration.
double *	GetIntegrationPointsWeightsBySets (unsigned long SetNumber, unsigned long &NumberIntegPoints)
	Returns the weights of the integration points. This method assumes that the weights have been already calculated by the procedure RunNumericalIntegration.
unsigned long *const	GetIndices (NumericalIntegrationAttributes_S &NIAttributes, unsigned long IntegrandOrder, unsigned long &NumIndices)
	Get indices for tensorization of numerical integration coordinates and weights. This method assumes that the indices have been already calculated by the procedure RunNumericalIntegration.
OneIndexTable< unsigned long > &	GetIndices ()
	Get indices for tensorization of numerical integration coordinates and weights. This method assumes that the indices have been already calculated by the procedure RunNumericalIntegration.
unsigned long *	GetIndicesBySet (unsigned long SetNumber, unsigned long &NumberIndices)
	Returns the tensor indices. This method assumes that the tensor indices have been already calculated by the procedure RunNumericalIntegration.
void	RunNumericalIntegration (NumericalIntegrationAttributes_S &NIAttributes, ElementShape_E EntityShape, BuiltInArray< unsigned long > &PolyOrder)
	Calculates the tensorization indices and the weigths for numerical integration of the polynomial orders given in the input parameter PolyOrder and integrand orders calculated by [1,IOFactor] * P..
void	Print (FILE *File, ElementShape_E EntityShape)
	: Prints the numerical integration attributes and values to the given ascii file.
Protected Attributes
LineNumericalIntegration	LineNI
	Instance of the LineNumericalIntegration class used to store the line coordinates and weights for the isoparametric coordinates. This is used to calculate the edge loads for triangles.
LineNumericalIntegration	LineNI1
	Instance of the LineNumericalIntegration class used to store the line coordinates and weights in direction L1.
LineNumericalIntegration	LineNI2
	Instance of the LineNumericalIntegration class used to store the line coordinates and weights in direction L2.
LineNumericalIntegration	LineNI3
	Instance of the LineNumericalIntegration class used to store the line coordinates and weights in direction L3.
OneIndexTable< double >	Weights
	Table to store the triangle integration weights for all polynomial orders P and integrand orders calculated as [1,IOFactor] * P.
OneIndexTable< double >	Coords
	Table that stores the integration points coordinates for triangles.
OneIndexTable< unsigned long >	TensorIndices
	Table to store the tensorization indices p, q and r for every integration point of the triangle element and polynomial order.
unsigned long	Pmax

Detailed Description

Calculates the coordinates and weights for numerical integration of the triangle element. The coordinates are those ones mapped from the square element to the baricentric coordinates of the triangle.

Author:: Fabiano Fernandes Bargos/Marco Lcio Bittencourt

Date:: March/15/2011

Note:: Only the tensorization indices and weights are stored. The coordinates are collected from the line coordinates only if they are necessary. There is not variable to store the coordinates for triangles, only for the lines.

Constructor & Destructor Documentation

TriangleNumericalIntegration::TriangleNumericalIntegration ( TriangleNumericalIntegration & Instance )

Copy-initializer constructor.

Parameters:

[in] Instance - instance of the TriangleNumericalIntegration class

Member Function Documentation

unsigned long *const TriangleNumericalIntegration::GetIndices	(	NumericalIntegrationAttributes_S &	NIAttributes,
		unsigned long	IntegrandOrder,
		unsigned long &	NumIndices
	)

Get indices for tensorization of numerical integration coordinates and weights. This method assumes that the indices have been already calculated by the procedure RunNumericalIntegration.

Parameters:

[in]	IntegrandOrder	- order of the integrand. Based on this value, the number of integration points is calculated for the quadrature rule stored in the class data.
[out]	NumberIndices	- number of tensorization indices.

Returns:: Pointer to the array of indices.

OneIndexTable< unsigned long > & TriangleNumericalIntegration::GetIndices ( )

Get indices for tensorization of numerical integration coordinates and weights. This method assumes that the indices have been already calculated by the procedure RunNumericalIntegration.

Returns:: a OneIndexTable<unsigned long>& type.

unsigned long * TriangleNumericalIntegration::GetIndicesBySet	(	unsigned long	SetNumber,
		unsigned long &	NumberIndices
	)

Returns the tensor indices. This method assumes that the tensor indices have been already calculated by the procedure RunNumericalIntegration.

Parameters:

[in]	SetNumber	- the set number.
[out]	NumberIndices	- number of tensor indices

Returns:: Pointer to the array with the tensor indices.

double *const TriangleNumericalIntegration::GetIntegrationPointsCoords	(	NumericalIntegrationAttributes_S &	NIAttributes,
		unsigned long	EntityShape,
		unsigned long	IntegrandOrder,
		unsigned long &	NumberIntegPoints,
		unsigned long	LiDirection = `1`
	)

Returns the coordinates of the integration points. In the case of Shape=TRIANGLE, this method collects the coordinates for the triangle element from the coordinates of the line everytime the method is executed.

Parameters:

[in]	EntityShape	- entity shape for which the coordinates of the integration points must be returned. For example, the element shape is SQUARE, but only the edge points are required. In this case, EntityShape must be LINE.
[in]	IntegrandOrder	- order of the integrand. Based on this value, the number of integration points are calculated for the quadrature rule stored in the class data.
[out]	NumberIntegrationPoints	- number of integration points
[in]	LiDirection	- Baricentric direction number.

Returns:: Pointer to the array with the coordinates.

long TriangleNumericalIntegration::GetIntegrationPointsSetNumber	(	NumericalIntegrationAttributes_S &	NIAttributes,
		unsigned long	IntegrandOrder
	)

Returns the set number of the integration points for the given polynomial order.

Parameters:

[in] PolyOrder - polynomial order

Returns:: a long type with the set number value.

double *const TriangleNumericalIntegration::GetIntegrationPointsWeights	(	NumericalIntegrationAttributes_S &	NIAttributes,
		ElementShape_E	EntityShape,
		unsigned long	IntegrandOrder,
		unsigned long &	NumberIntegPoints,
		unsigned long	LiDirection = `1`
	)

Returns the weights of the integration points. This method assumes that the weights have been already calculated by the procedure RunNumericalIntegration.

Parameters:

[in]	EntityShape	- entity shape for which the weiths of integration points must be returned. For example, the element shape is SQUARE, but only the edge points are required. In this case, EntityShape must be LINE.
[in]	IntegrandOrder	- order of the integrand. Based on this value, the number of integration points are calculated for the quadrature rule stored in the class data.
[out]	NumberIntegPoints	- number of integration points.
[in]	LiDirection	- Baricentric direction number.

Returns:: Pointer to the array with the weights

double * TriangleNumericalIntegration::GetIntegrationPointsWeightsBySets	(	unsigned long	SetNumber,
		unsigned long &	NumberIntegPoints
	)

Returns the weights of the integration points. This method assumes that the weights have been already calculated by the procedure RunNumericalIntegration.

Parameters:

[in] SetNumber - Number of the desired set of integration points

param[out] NumberIntegPoints - number of integration points.

Returns:: Pointer to the array with the weights for the given set.

LineNumericalIntegration & TriangleNumericalIntegration::GetLineNumericalIntegration ( unsigned long LiDirection = 1 )

Returns the reference to LineNumericalIntegration. According to LiDirection parameter returns one of the Line attributes of the class TriangleNumericalIntegration. If the direction is 0, it returns the numerical integration on the isoparametric coordinates.

Parameters:

[in] LiDirection - Baricentric direction number.

Returns:: LineNumericalIntegration& - reference to the class LineNumericalIntegration.

unsigned long TriangleNumericalIntegration::GetMaxNumberIntegrationPointsSets ( unsigned long LiDirection = 1 )

Returns the maximum number of sets of integration points according to LineNI[1-3] class attributes.

Parameters:

[in] LiDirection - Baricentric direction number.

Returns:: the maximum number of sets as an unsigned long.

unsigned long TriangleNumericalIntegration::GetMaxPolyOrder ( )

Returns the maximum polynomial order.

Returns:: Maximum polynomial order as an unsigned long.

unsigned long TriangleNumericalIntegration::GetNumberIntegrationPoints	(	NumericalIntegrationAttributes_S &	NIAttributes,
		ElementShape_E	EntityShape,
		unsigned long	IntegrandOrder,
		long &	IntegPointsSetNumber
	)

Returns the number of integration points given by integrand order for the quadrature rule stored in the class. Returns also the number of the set which stores the points.

Parameters:

[in]	EntityShape	- entity shape for which the number of integration points must be returned. For example, the element shape is SQUARE, but only the edge points are required. In this case, EntityShape must be LINE.
[in]	IntegrandOrder	- order of the integrand. Based on this value, the number of integration points is calculated for the quadrature rule stored in the class data.
[out]	IntegPointsSetNumber	- number of the integration point set which stores the coordinates.

Returns:: Number of integration points as an unsigned long

unsigned long TriangleNumericalIntegration::GetNumberIntegrationPoints	(	ElementShape_E	EntityShape,
		long	IntegrationPointsSetNumber,
		unsigned long	LiDirection = `1`
	)

Returns the number of integration points for a given set number to a specific baricentric direction number.

Parameters:

[in]	EntityShape	- entity shape for which the integration points must be returned. For example, the element shape is SQUARE, but only the edge points are required. In this case, EntityShape must be LINE.
[in]	IntegrationPointsSetNumber	- number of the integration point set which stores the coordinates.
[in]	LiDirection	- Baricentric direction number.

Returns:: the number of integration points for a given set number as an unsigned long. If the set number is not used, returns 0.

unsigned long TriangleNumericalIntegration::GetNumberIntegrationPointsSets ( )

Returns the number of sets of integration points calculated using the polynomial and integration orders.

Returns:: Number of sets as an unsigend long

unsigned long TriangleNumericalIntegration::GetTotalNumberIntegrationPoints ( )

Returns the total number of integration points.

Returns:: an unsigned long with the total number of integration points value.

TriangleNumericalIntegration::operator LineNumericalIntegration & ( )

Cast operator for the reference of the class attribute "LineNI".

Returns:: reference to the class attribute "LineNI" of type LineNumericalIntegration

TriangleNumericalIntegration & TriangleNumericalIntegration::operator= ( TriangleNumericalIntegration & Instance )

Copies the contents of instance to the object.

Parameters:

[in] Instance - instance of the TriangleNumericalIntegration class

Returns:: Instance of the TriangleNumericalIntegration class

void TriangleNumericalIntegration::Print	(	FILE *	File,
		ElementShape_E	EntityShape
	)

: Prints the numerical integration attributes and values to the given ascii file.

Parameters:

[in]	File	- pointer to the ascii file
[in]	EntityShape	- entity shape for which the attributes of the integration points must be printed.

void TriangleNumericalIntegration::RunNumericalIntegration	(	NumericalIntegrationAttributes_S &	NIAttributes,
		ElementShape_E	EntityShape,
		BuiltInArray< unsigned long > &	PolyOrder
	)

Calculates the tensorization indices and the weigths for numerical integration of the polynomial orders given in the input parameter PolyOrder and integrand orders calculated by [1,IOFactor] * P..

Parameters:

[in]	NIAttributes	- parameters of the quadrature rule.
[in]	EntityShape	- entity shape for which the weights and coordinates integration points must be calculated. For example, the element shape is SQUARE, but only the edge points are required. In this case, EntityShape must be LINE.
[in]	PolyOrder	- element orders for a p-nonuniform mesh in an increasing sequence. For a p-uniform, this array stores only one value

void TriangleNumericalIntegration::SetMaxPolyOrder ( unsigned long MaxPolyOrder )

Sets the maximum polynomial order.

Parameters:

[in] MaxPolyOrder - maximum polynomial order.

void TriangleNumericalIntegration::SetNumberCoordsWeights	(	unsigned long	NumberRow,
		unsigned long	NumberData
	)

Sets the coordinates and weights table for the specific TriangleNumericalIntegration allocated.

Parameters:

[in]	NumberRow	- Number of table row.
[in]	NumberData	- Number of table coefficients.

The documentation for this class was generated from the following files:

include/interpolation/numericalintegration/TriangleNumericalIntegration.h
src/interpolation/numericalintegration/TriangleNumericalIntegration.cpp

Public Member Functions

Protected Attributes

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation